Dining Philosophers
Deadlock
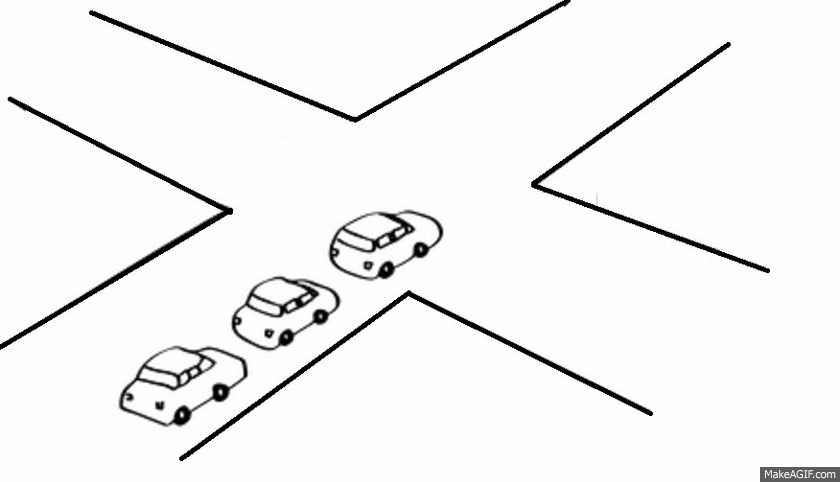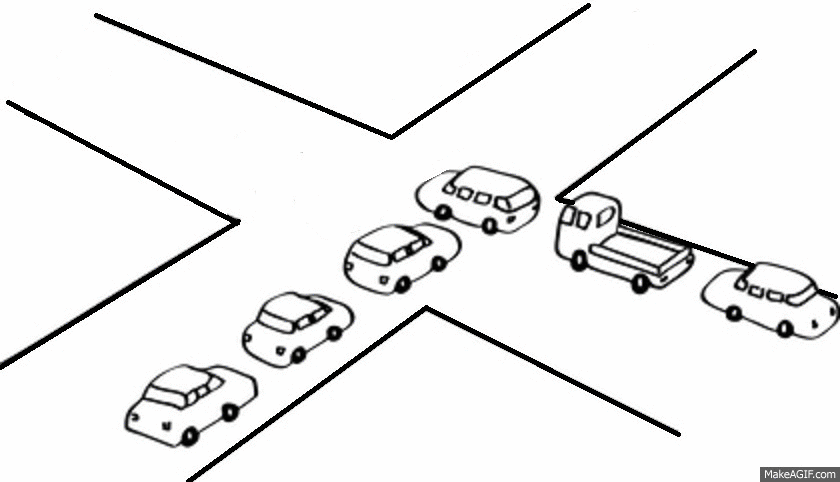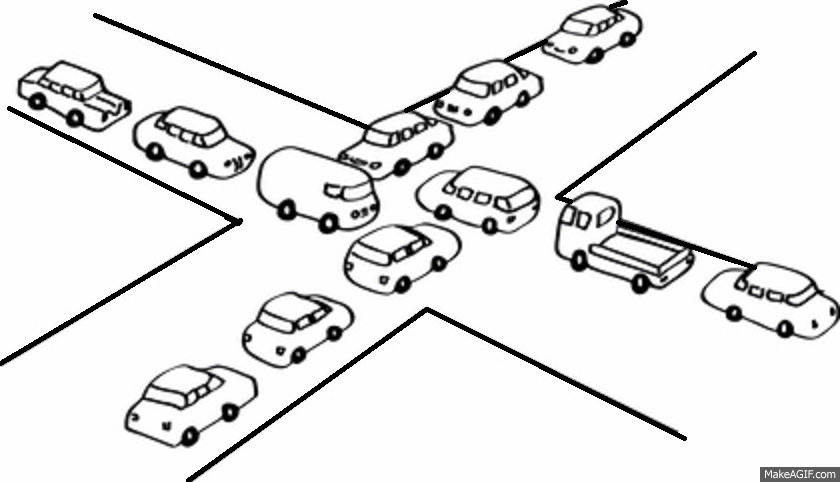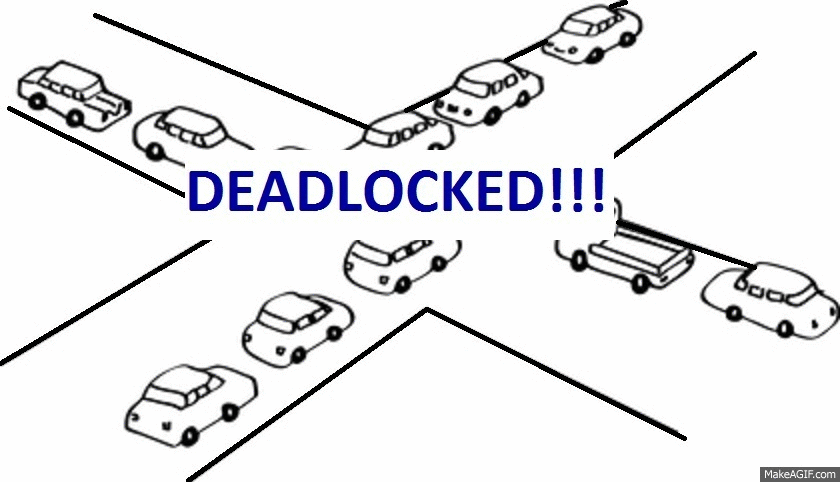
Dining philosophers
A good example of deadlock is the dining philosophers problem

Who’s a good Dining Philosopher

A Good Overview
What is deadlock?
From wikipedia:
In an operating system, a deadlock occurs when a process or thread enters a waiting state because a requested system resource is held by another waiting process, which in turn is waiting for another resource held by another waiting process. If a process is unable to change its state indefinitely because the resources requested by it are being used by another waiting process, then the system is said to be in a deadlock.
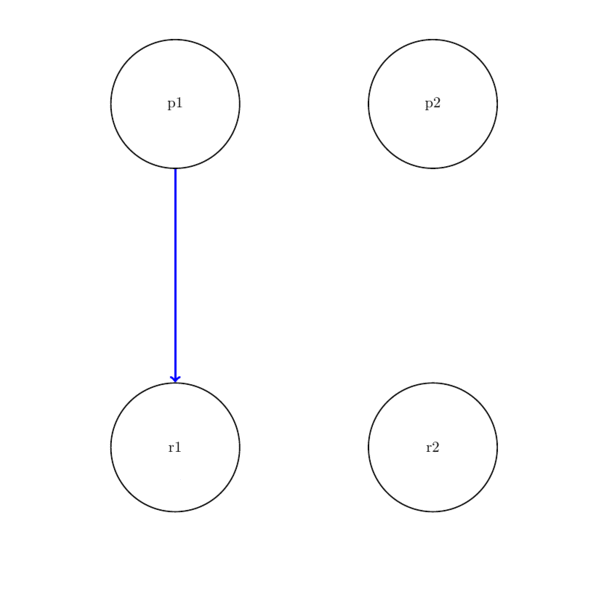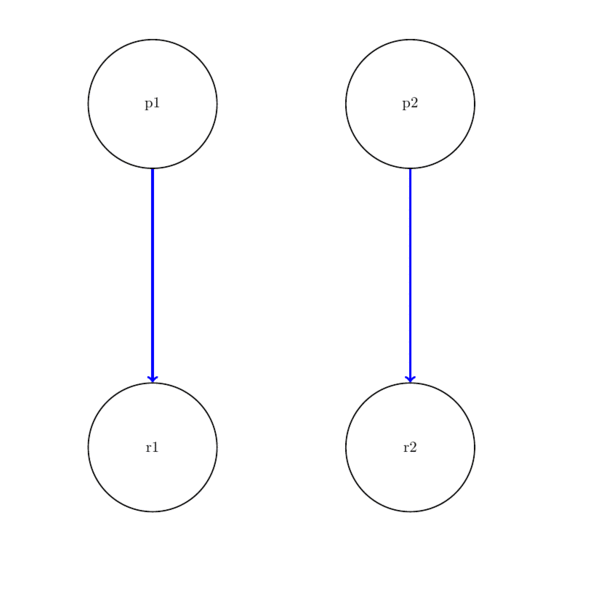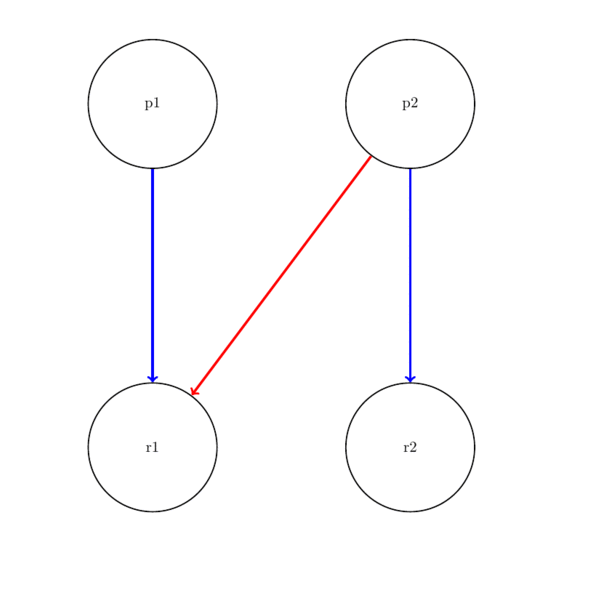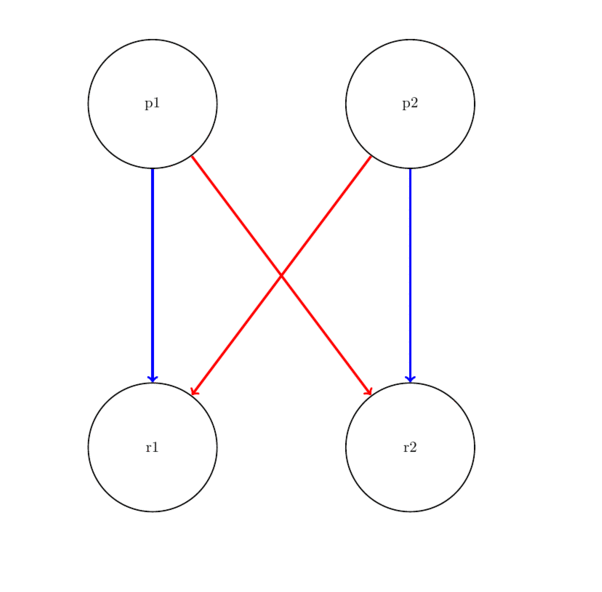
Resource allocation graph
We can model resource allocation by having resources and processes represented as vertices and use edges to show ownership of a resource. A cycle in the (undirected) resource allocation graph implies that we have deadlock.
Example RAG
Solutions to the dining philsophers problem
Arbitrator
Have one authority (mutex in the case of c). Have each philosopher grab that authority and only when they have the authority can they pick up their forks and eat. They eat, put the arbitrator and the forks down and move on to the next philosopher (can be random or sequential).
Downsides
- Very slow
- Only one thread running at a time essentially
- This is python’s GIL in a nutshell
Leave the table (Stallings)
Reduce the case of the dining philosophers to a case of n-chopsticks and p-philosophers. Reduce the number of philosophers currently allowed at the table to n-1. Have them eat. Cycle out the philosophers.
Downsides
- Very heavy on context switchings for process
- Needs way of keeping the philosophers at bay (SIGSTOP for linux kernel)
- Needs some cycling algorithm
Partial Ordering (Dijkstra)
Order the chopsticks 1..n. For each philosopher have them pick up the lower number chopstick. Then, only if they can pick up the lower chopstick, pick up the higher chopstick. Why does this work?
Downsides
- Needs to be able to order the resources
- Doesn’t livelock but often leads one thread working at a time for large applications (databases)
- But good for dining philosophers!
Clean/Dirty (Chandra/Misra)
If you want reeealllllllly fast (Given a lot of philosophers).